Kružnice a kruh
Kružnice je množina všech bodů v rovině, které leží ve stejné vzdálenosti (poloměr kružnice) od pevně daného bodu (střed kružnice). Kružnice rozděluje rovinu na vnitřek a vnějšek. Kruh je množina bodů složená nejen z kružnice, ale i z jejího vnitřku.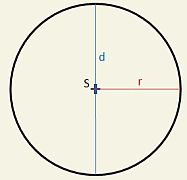
Značení kružnice
| S | střed kružnice / kruhu |
| r | poloměr kružnice / kruhu |
| d | průměr kružnice / kruhu (=2*r) |
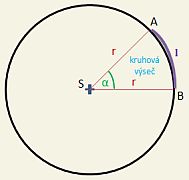
| |ASB| | kruhová výseč (vnitřní prostor ohraničený poloměry r a obloukem l) |
| l | délka oblouku (určeného body A,B) |
| α | středový úhel |
Vlastnosti kružnice a kruhu
|
Obsah (plocha) a obvod kružnice / kruhu, kruhová výseč a mezikruží
|
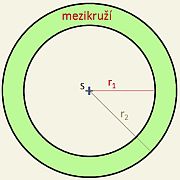
obvod o = 2πr nebo o = πd obsah kruhu S = πr2 délka kruhového oblouku l = (2πr) / 360° × α nebo l = r×x, kde x = velikost úhlu v radiánech obsah kruhové výseče Sv = (πr2) / 360° × α nebo Sv = (r2/2) × (x-sin(x)), kde x = velikost úhlu v radiánech obsah mezikruží Sm = π × (r22-r12), kde r2 je poloměr větší kružnice a r1 té menší |
Zdroj: Wikipedia.org, Matematika.cz, Planimetrie.chytrak.cz, 2014
| Planimetrie, rovinné útvary |
 Trojúhelník -
 Čtverec -
 Obdélník -
 Kružnice a kruh  Rovnoběžník, Kosodélník -
 Lichoběžník -
 Kosočtverec -
 Pravidelný pětiúhelník -
 Pravidelný šestiúhelník  Vzorečky (obvody, obsahy, atp.)
|
Informace na tomto webu jsou veřejně dostupné a čerpají z různých zdrojů, které jsou uvedeny.
Autor webu (petr@skaut.cz) nenese odpovědnost za případné použití chybných informací.
Autor webu (petr@skaut.cz) nenese odpovědnost za případné použití chybných informací.