Pravidelný pětiúhelník, pentagon
Jedná se o rovinný útvar, který má pět stejně dlouhých stran a pět vrcholů, jejichž vnitřní úhel je vždy 108°. Říká se mu také pentagon.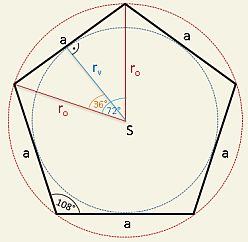
Značení pravidelného pětiúhelníku, pentagonu
| a | strany pětiúhelníku (všechny stejně dlouhé) |
| ro | poloměr kružnice opsané (vnější) |
| rv | poloměr kružnice vepsané (vnitřní) |
| S | obsah pětiúhelníku |
| o | obvod pětiúhelníku (součet všech stran - jsou shodné, takže 5*a) |
Vlastnosti pravidelného pětiúhelníku, pentagonu
|
Obsah (plocha) a obvod pravidelného pětiúhelníku, pentagramu
|
obvod o = 5*a obsah S = [ √( 25 + 10√5 ) / 4 ] * a2 poloměr kružnice opsané (vnější) ro = [ √( 50 + 10√5 ) / 10 ] * a poloměr kružnice vepsané (vnitřní) rv = [ √( 25 + 10√5 ) / 10 ] * a |
Konstrukce pětiúhelníku, pentagonu
Postup, jak sestrojit pětiúhelník za pomoci kružítka a pravítka. Snažil jsem se ho napsat vlastními slovy tak, aby byl co nejlépe pochopitelný, takže snad prominete, pokud tam budou matematicky nepřesné výrazy :-)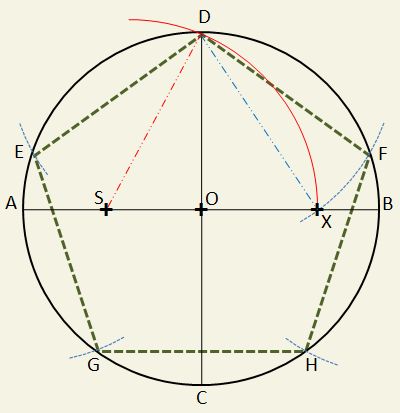
|
Zdroj: Wikipedia.org, 2014
Vypocitejto.cz, 2014
| Planimetrie, rovinné útvary |
 Trojúhelník -
 Čtverec -
 Obdélník -
 Kružnice a kruh  Rovnoběžník, Kosodélník -
 Lichoběžník -
 Kosočtverec -
 Pravidelný pětiúhelník -
 Pravidelný šestiúhelník  Vzorečky (obvody, obsahy, atp.)
|
Informace na tomto webu jsou veřejně dostupné a čerpají z různých zdrojů, které jsou uvedeny.
Autor webu (petr@skaut.cz) nenese odpovědnost za případné použití chybných informací.
Autor webu (petr@skaut.cz) nenese odpovědnost za případné použití chybných informací.