Rovnoběžník
Zvaný též kosodélník, je čtyřúhelník, jehož protější strany jsou rovnoběžné, jeho vnitřní úhly jsou zpravidla nepravoúhlé. V případě pravoúhlých vnitřních úhlů se pak jedná o obdélník. Pokud úhly nejsou pravé, ale všechny strany jsou stejně dlouhé, hovoříme o kosočtverci. Jsou-li splněny obě podmínky dohromady, pak se jedná o čtverec .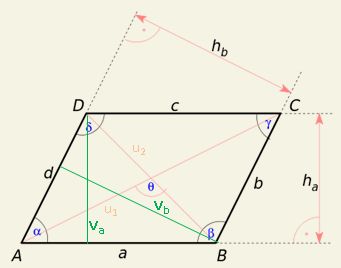
Značení rovnoběžníku
| A,B,C,D | vrcholy rovnoběžníku |
| a,b (někdy i c,d) | strany obdélníku (protější strany stejně dlouhé a rovnoběžné) |
| α,β,γ,δ | vnitřní úhly rovnoběžníku (protější úhly jsou shodné) |
| u1,u2 | úhlopříčky rovnoběžníku |
| va,vb | výšky rovnoběžníku, někdy se značí také ha,hb |
| S | obsah rovnoběžníku (nejjednodušeji: a * výška strany) |
| o | obvod rovnoběžníku (součet všech stran, tedy 2*a+2*b) |
Vlastnosti rovnoběžníku / kosodélníku
|
Obsah (plocha) a obvod rovnoběžníku
|
obvod o = 2*a + 2*b obsah S = a*va obsah při známé velikosti stran a jejich vnitřního úhlu S = a*b*sin(α) Složitější vzorce hledejte ve zdrojích ;-) |
Zdroj: Wikipedia.org, 2014
| Planimetrie, rovinné útvary |
 Trojúhelník -
 Čtverec -
 Obdélník -
 Kružnice a kruh  Rovnoběžník, Kosodélník -
 Lichoběžník -
 Kosočtverec -
 Pravidelný pětiúhelník -
 Pravidelný šestiúhelník  Vzorečky (obvody, obsahy, atp.)
|
Informace na tomto webu jsou veřejně dostupné a čerpají z různých zdrojů, které jsou uvedeny.
Autor webu (petr@skaut.cz) nenese odpovědnost za případné použití chybných informací.
Autor webu (petr@skaut.cz) nenese odpovědnost za případné použití chybných informací.